7747. Городской горизонт
Фермер Джон приехал со своими
коровами в город! Во время захода солнца коровы смотрят на городской горизонт и
наблюдают красивые силуэты, образованные прямоугольными зданиями.
Весь горизонт представлен числовой
прямой с n (1 ≤ n ≤ 40000) зданиями. Силуэт i-го здания распростерся вдоль горизонта
между точками ai и bi (1 ≤ ai < bi ≤ 109) и имеет высоту hi (1 ≤ hi ≤ 109).
Определите площадь в квадратных единицах общего силуэта, образованного всеми n зданиями.
Вход. Первая
строка содержит целое число n. Каждая
из следующих n строк описывает здание
i тремя целыми числами: ai, bi и
hi.
Выход. Выведите
общую площадь городского силуэта в квадратных единицах, образованного всеми n зданиями.
|
Пример входа |
Пример выхода |
|
4 2 5 1 9 10 4 6 8 2 4 6 3 |
16 |
РЕШЕНИЕ
заметающая прямая
Анализ алгоритма
Отсортируем
точки – абсциссы начал и концов зданий по возрастанию. С каждой точкой запомним,
является ли она началом (type = 0)
или концом (type = 1) здания, а также
высоту самого здания. Будем последовательно обрабатывать точки слева направо.
В
мультимножестве s храним высоты зданий, которые на данный момент уже начались,
но еще не закончились. Мультимножество будет поддерживать высоты по убыванию.
Пусть
на данный момент мы находимся в точке xi.
Пусть h – наибольшее число в
мультимножестве. Это значит, что текущее (на
интервале [xi, xi+1]) самое
высокое здание имеет высоту h
(которое еще не закончилось). Добавим к площади горизонта значение (xi+1 – xi) * h. Если точка xi
– начало здания, то соответствующую ей высоту добавим в мультимножество. Если точка
xi конец здания, то удалим из мультимножества его высоту. Порядок
обработки начал и концов зданий с одинаковыми абсциссами не имеет значения.
Пример
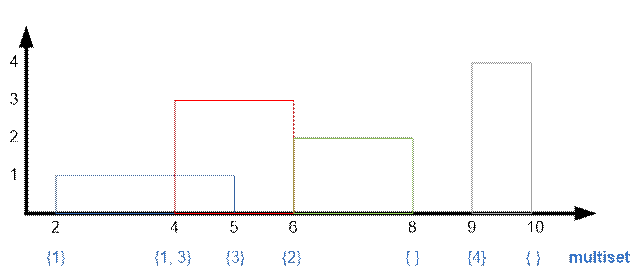
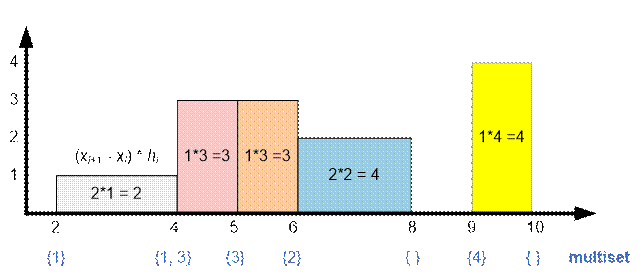
Реализация алгоритма
Для точки объявим структуру node, которая будет
хранить ее абсциссу x, информацию
является ли она началом (type = 0) или концом (type =
1) отрезка, а также высоту h соответствующего
здания.
struct node
{
int x, type, h;
node(int x, int type, int h) : x(x), type(type), h(h) {};
};
Определим компаратор f для точек – сортировать их будем по абсциссам.
int f(node a, node b)
{
return a.x < b.x;
}
Объявим массив точек Event, а также мультимножество s
для хранения высот зданий, пересекающихся с текущей абсциссой сканирующей
прямой.
vector<node> Event;
multiset<int,
greater<int> > s;
Читаем входные данные. Строим массив точек.
scanf("%d",&n);
for(i = 0; i
< n; i++)
{
scanf("%d %d %d",&left,&right,&height);
Event.push_back(node(left,0,height));
Event.push_back(node(right,1,height));
}
Сортируем массив точек по неубыванию абсцисс.
sort(Event.begin(),Event.end(),f);
В переменной res подсчитываем общую площадь
городского силуэта.
res = 0;
Двигаемся слева направо по точкам массива Event. Для каждого значения i for цикла
рассматриваем инервал (Event[i].x, Event[i + 1].x).
for (i = 0; i < Event.size() - 1; i++)
{
Если точка xi
– начало здания, то соответствующую ей высоту добавим в мультимножество.
int h = Event[i].h;
if (Event[i].type == 0) s.insert(h);
Если точка xi – конец здания, то удалим из мультимножества
соответствующую ей высоту.
else s.erase(s.find(h));
Если стек не пустой, то между точками Event[i].x и Event[i + 1].x
имеется линия горизонта, высота которой равна наибольшему значению в
мультимножестве s, а именно
значению *s.begin().
if (!s.empty())
res += 1LL * *s.begin() *
(Event[i+1].x - Event[i].x);
}
Выводим искомую площадь.
printf("%lld\n",res);
Реализация при помощи дерева
отрезков
Сожмем абсциссы зданий при помощи отображения mp (mp[2]
= 1, mp[4] = 2 и так далее). Построим дерево отрезков [1..len], где len ≤ 40000.
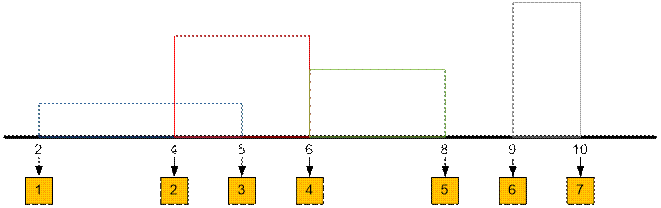
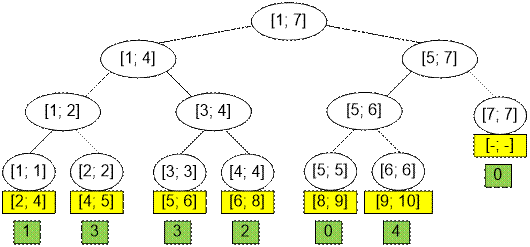
Каждый лист дерева отрезков соответствует одному
неделимому интервалу силуэта на горизонте. Например, вершина 1 соответствует интервалу
[2; 4], вершина 2 соответствует интервалу [4; 5]. Тогда отрезок [a, b]
покрывается вершинами [mp[a], mp[b] – 1] из дерева отрезков. Например,
отрезок [2; 5]
покрывается вершинами [mp[2], mp[5] – 1] = [1, 2].
Для каждого здания на отрезке [ai,
bi] высоты hi увеличим на hi все значения дерева
отрезков на интервале [mp[ai],
mp[bi] – 1]. При проталкивании значения
в вершине поддерживаем максимум:
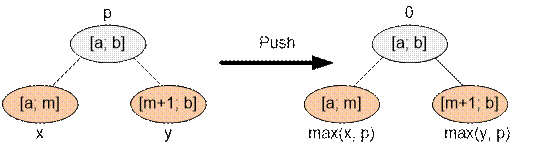
Протолкнем все значения вершин до листьев, после чего
листы будут содержать высоты силуэта на интервалах. Например, первый лист
соответствует отрезку [2; 4] и содержит значение 1, второй лист соответствует
отрезку [4; 5] и содержит значение 3 и так далее. Последняя вершина дерева
отрезков не соответствует никакому интервалу и является фиктивной.
#include <cstdio>
#include <cstring>
#include <set>
#include <map>
#include <vector>
#include <algorithm>
#define MAX 80010
using namespace std;
int
SegTree[4*MAX];
vector<int>
a;
map<int,int> mp;
int i, n, l,
r, h, len;
long long res;
struct Building
{
int left, right, height;
} b[40010];
void Push(int Vertex, int
LeftPos, int Middle, int
RightPos)
{
if (SegTree[Vertex])
{
SegTree[2*Vertex] = max(SegTree[2*Vertex],SegTree[Vertex]);
SegTree[2*Vertex+1] = max(SegTree[2*Vertex+1],SegTree[Vertex]);
SegTree[Vertex] = 0;
}
}
void Add(int Vertex, int
LeftPos, int RightPos,
int
Left, int Right, int
x)
{
if (Left > Right) return;
if ((LeftPos == Left) && (RightPos == Right))
SegTree[Vertex] = max(SegTree[Vertex],x);
else
{
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
Add(2*Vertex, LeftPos, Middle, Left, min(Middle,Right), x);
Add(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right, x);
}
}
long long Count(int
Vertex, int LeftPos, int
RightPos)
{
if (LeftPos == RightPos)
return 1LL * SegTree[Vertex] * (a[LeftPos+1] -
a[LeftPos]);
else
{
int Middle =
(LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
return Count(2*Vertex, LeftPos, Middle) +
Count(2*Vertex+1, Middle+1, RightPos);
}
}
int main(void)
{
scanf("%d",&n);
memset(SegTree,0,sizeof(SegTree));
set<int> s;
for(i = 1; i <= n; i++)
{
scanf("%d %d %d",&b[i].left,&b[i].right,&b[i].height);
s.insert(b[i].left); s.insert(b[i].right);
}
len =
s.size(); a.resize(len+2);
copy(s.begin(),s.end(),a.begin()+1);
for(i = 1; i <= len; i++) mp[a[i]] = i;
for(i = 1; i <= n; i++)
Add(1,1,len,mp[b[i].left],mp[b[i].right]-1,b[i].height);
res =
Count(1,1,len);
printf("%lld\n",res);
return 0;
}